Bayesian Approaches For Modeling Protein Biophysics

Keegan Hines

Aldrich Lab

Outline

Background


Parameter Identifiability in Nonlinear Biophysical Models


Modeling Single Molecule Time Series Using Nonparametric Bayesian Inference

Proteins

  • Fundamental unit of computation and signal processing in biological systems
  • Fold into complex structures which determine their function

Proteins

  • Proteins are dynamic, exploring very many conformational states.
  • What can we do to understand these dynamics?

Jensen et al., 2012, Mechanism of Voltage Gating in Potassium Channels, Science , 336, 6078.

Modeling Proteins

Physiological relevance- we only need to account for some of this complexity

Modeling Natural Systems

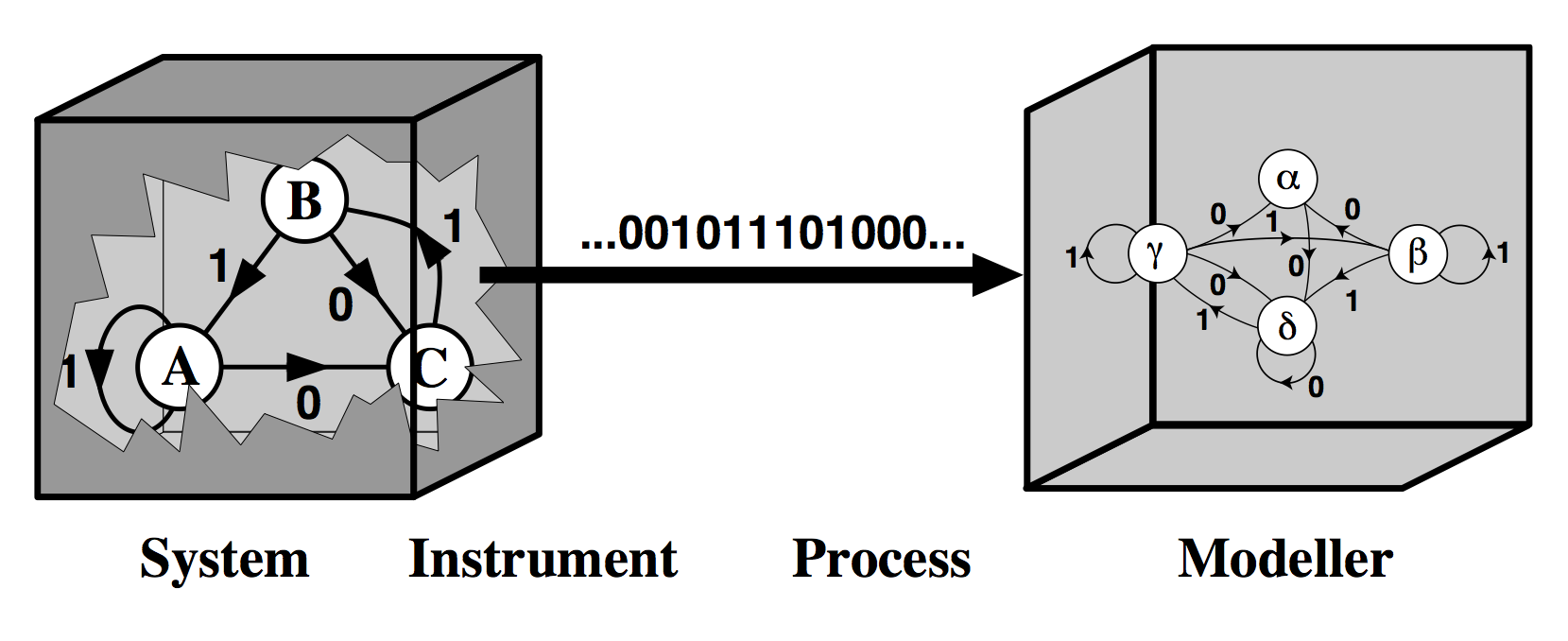
Imagery stolen from Jim Crutchfield lecture notes

Parameter Identifiability in Nonlinear Biophysical Models

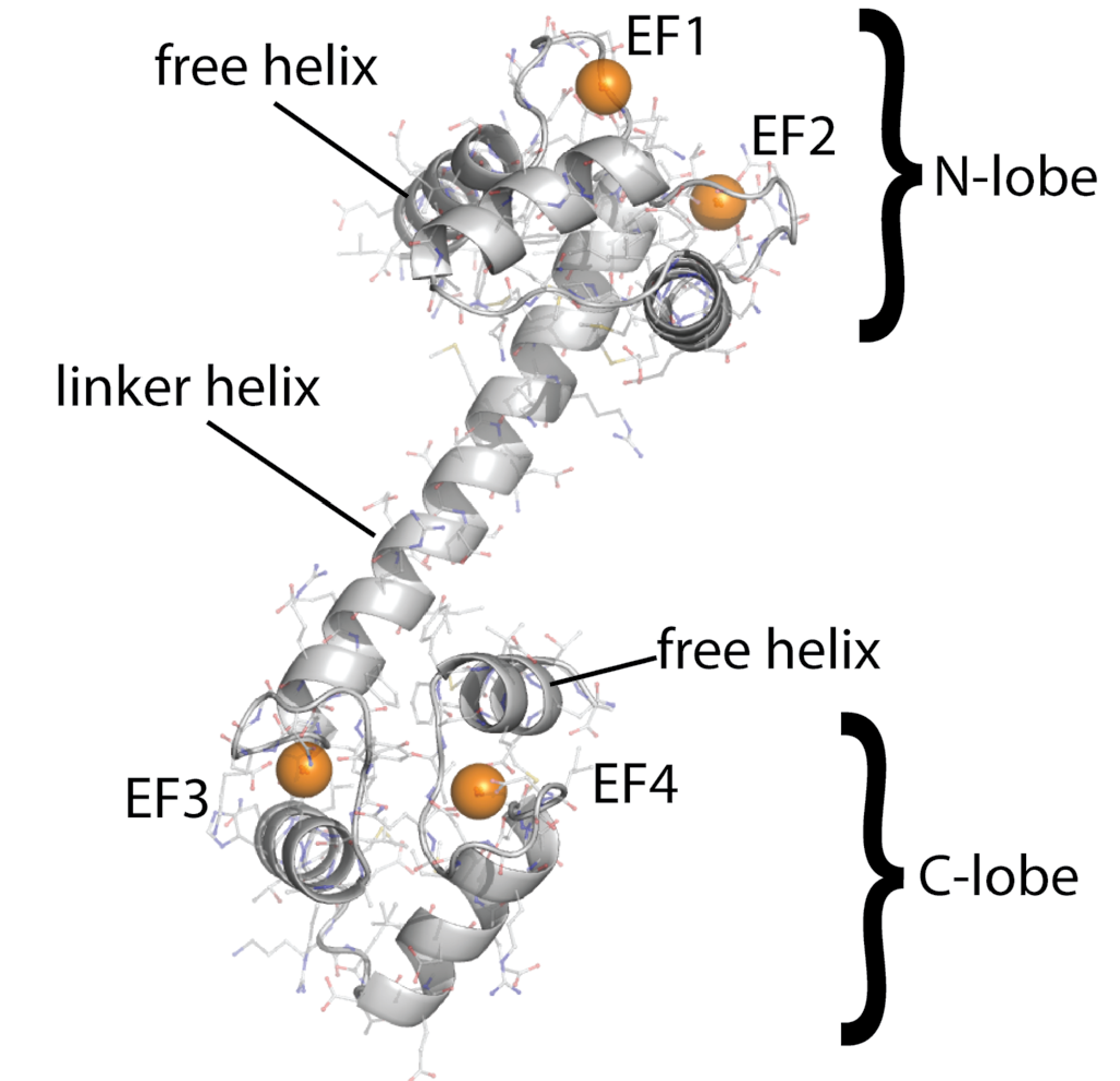
Calmodulin

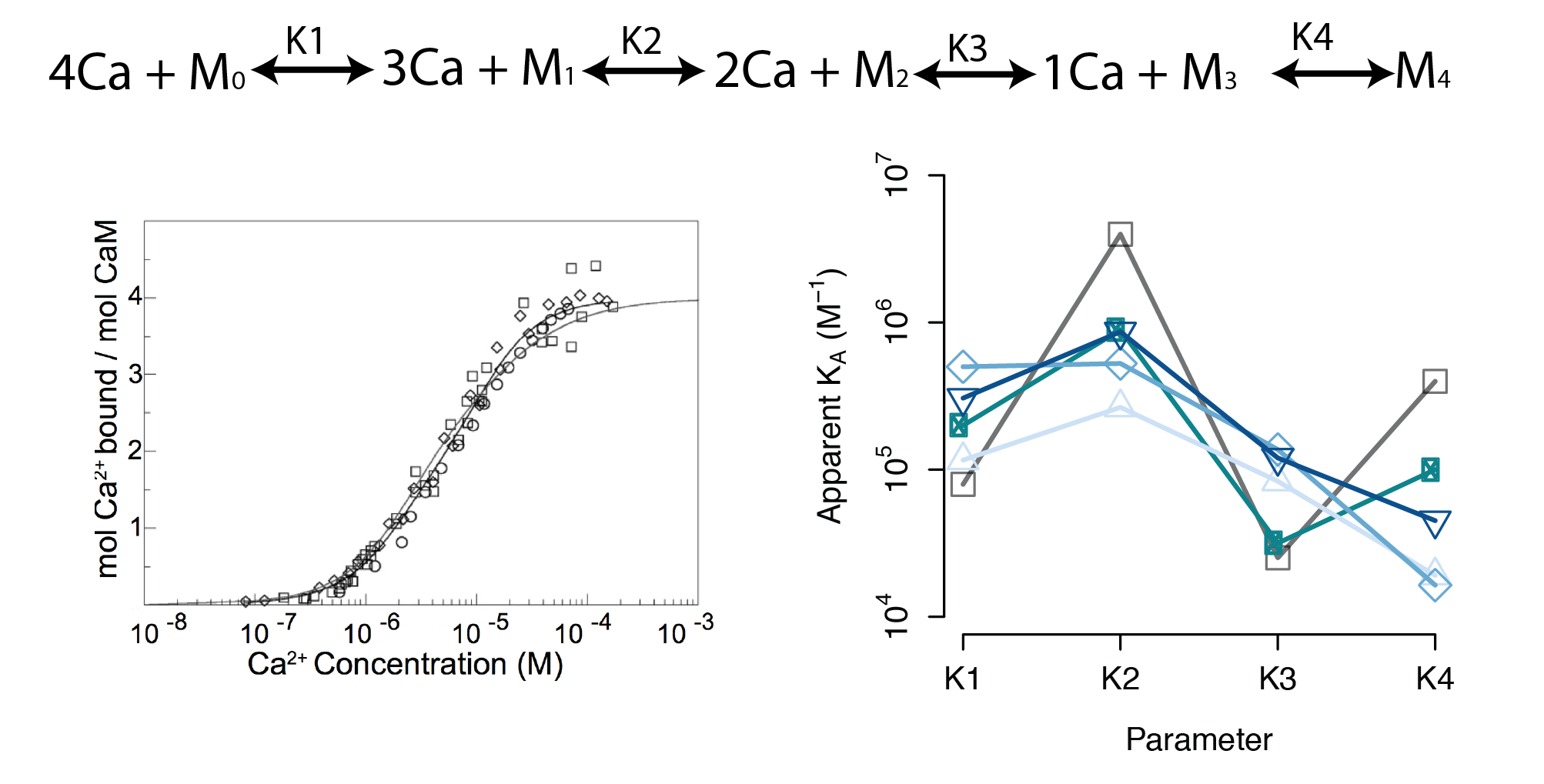
Calcium signaling via calmodulin plays a vital role in many biological processes including ion channel modulation and synaptic plasticity.

Calmodulin

  • A sequential binding model is often used to study CaM
  • Current estimates of binding parameters vary wildly

Stefan et al, 2009. Computing phenomenologic Adair-Klotz constants from microscopic MWC parameters. BMC Systems Biology. 3:68.

Sequential Binding Model

Large regions of this parameter space can fit any data extremely well

Parameter Identifiability

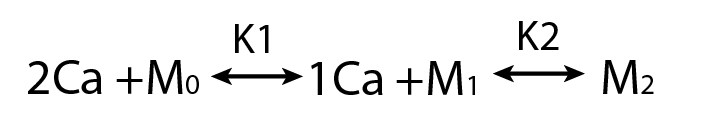
Parameter Identifiability

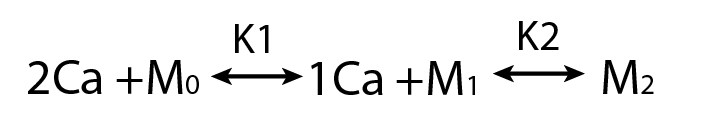
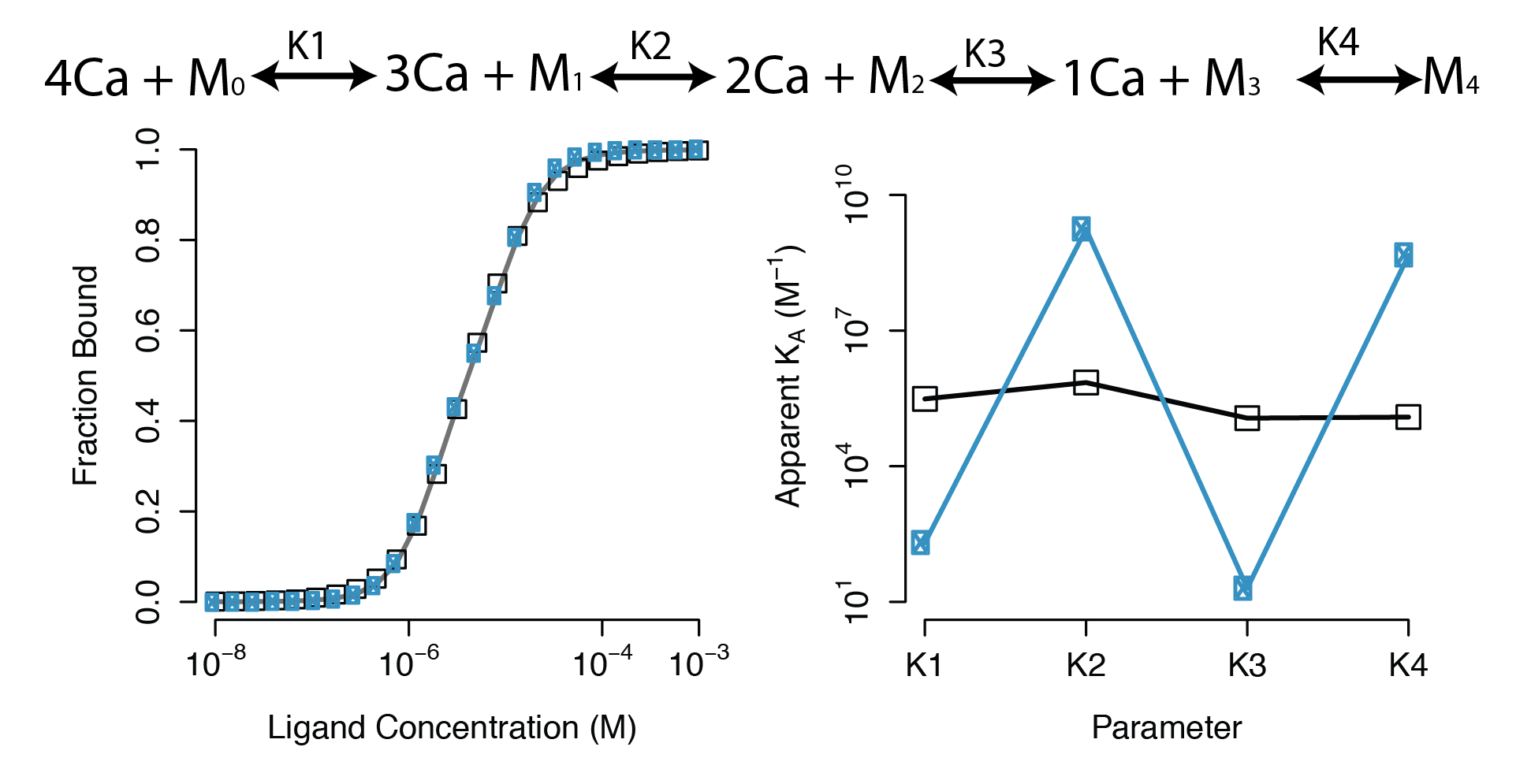
Practical Non-identifiability

Structural Non-identifiability

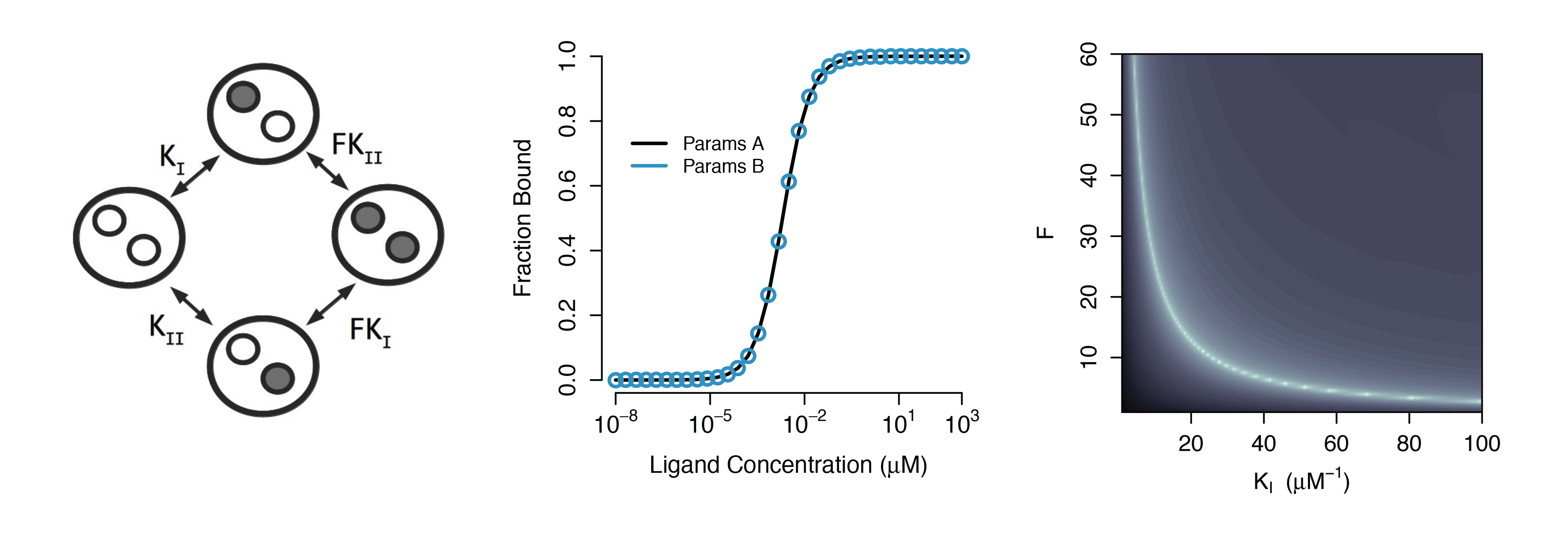
Parameters cannot be inferred accurately even with noiseless data

Identifying Identifiability

Analytical methods exist, but can only be used in special cases. Worse, such methods can be misleading, as in the case of practical non-identifiability.



We might calculate the Error (likelihood) over the whole parameter space, but this is infeasible for many parameters.



We need an efficent way to identify the regions of parameter space that lead to good agreement with the data.

Bayesian Inference

The posterior distribution quantifies which regions of the parameter space provide a good explanation of the data.


Bayes' rule specifies how to calculate posterior probability, and Markov chain Monte Carlo provides an efficient method to estimate high-dimensional posterior distributions.

Markov chain Monte Carlo

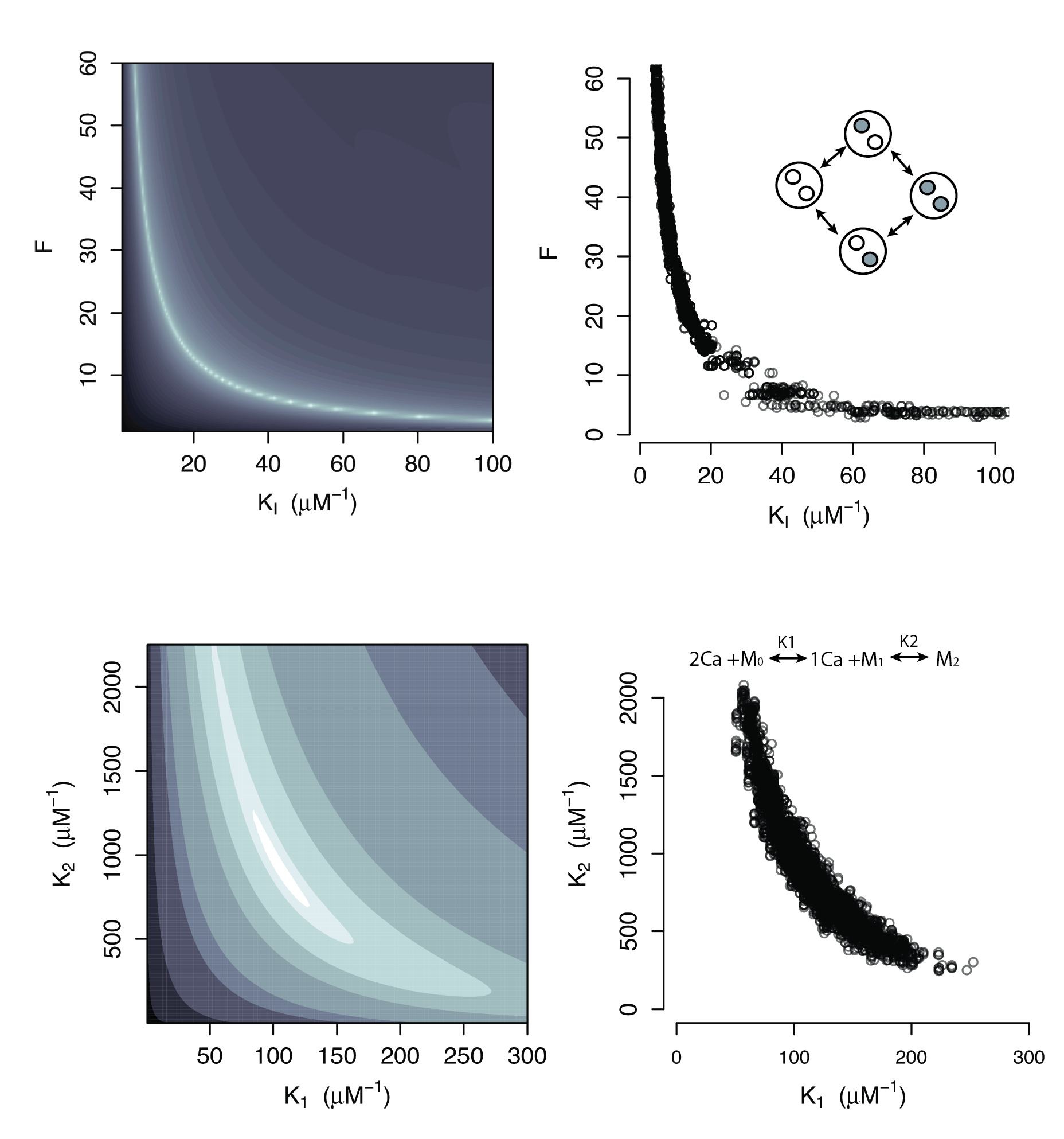
Additional Applications

Dynamical Systems

Additional Applications

Dynamical Systems

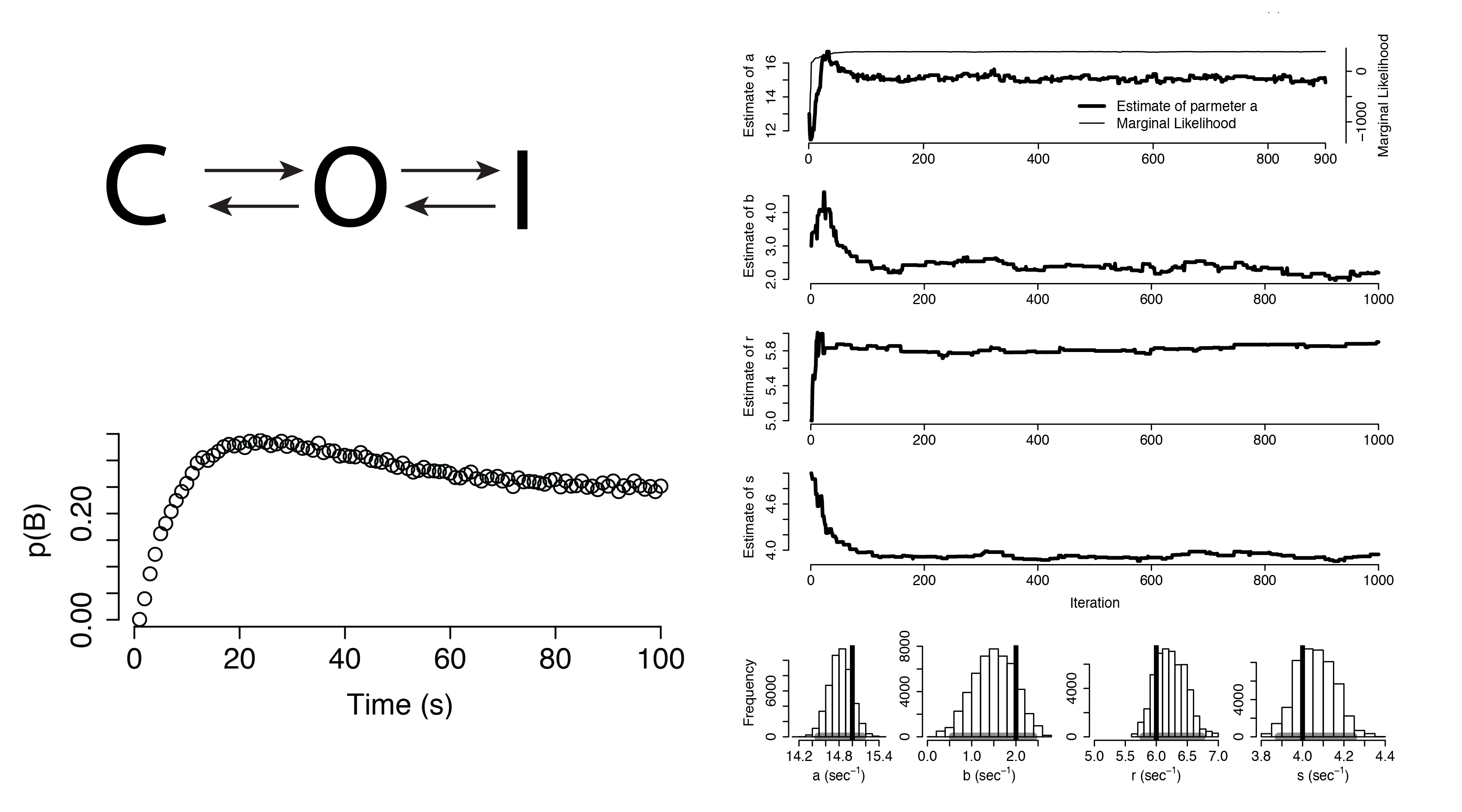
Additional Applications

Dynamical Systems

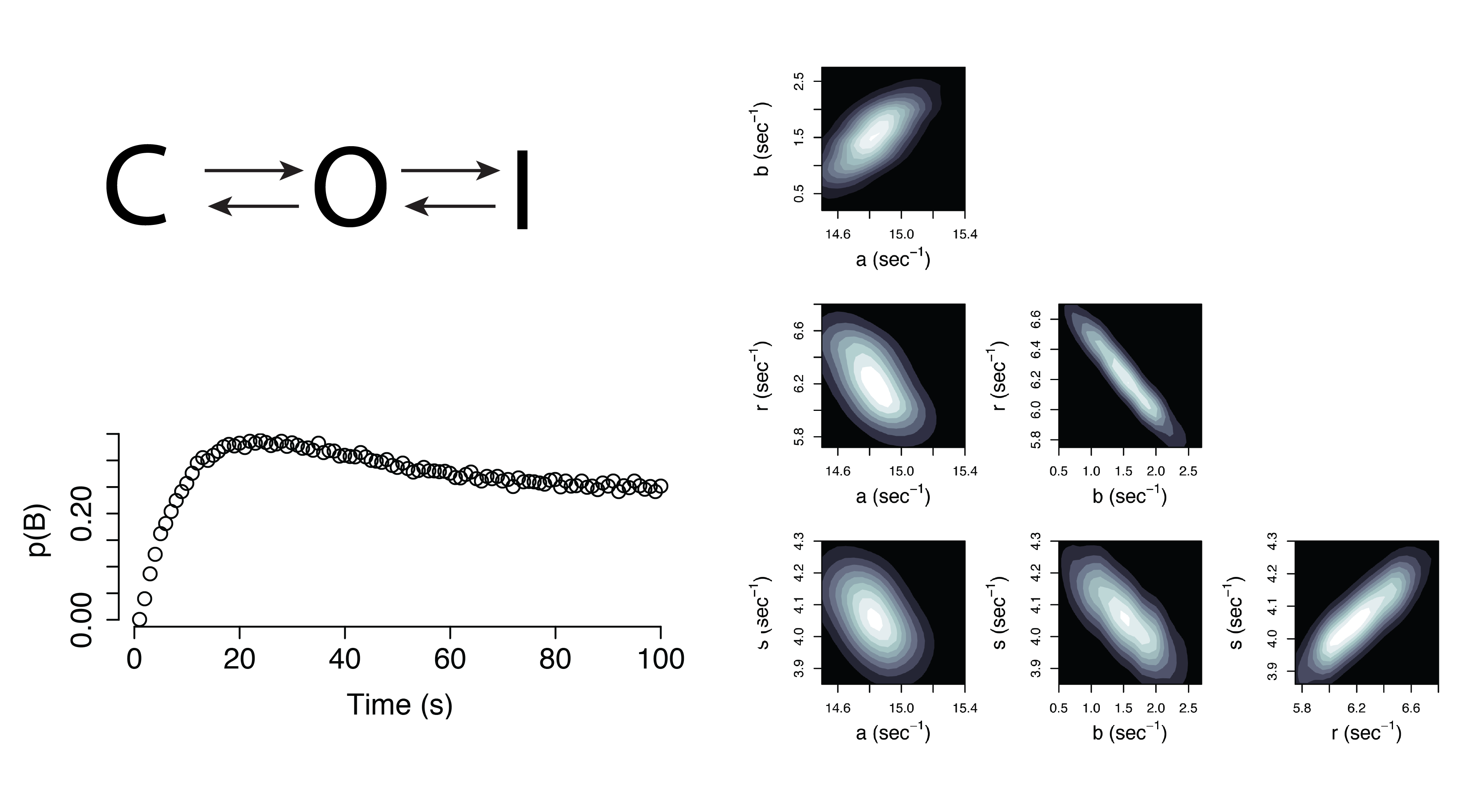
Additional Applications

Dynamical Systems (Non-Identifiable)

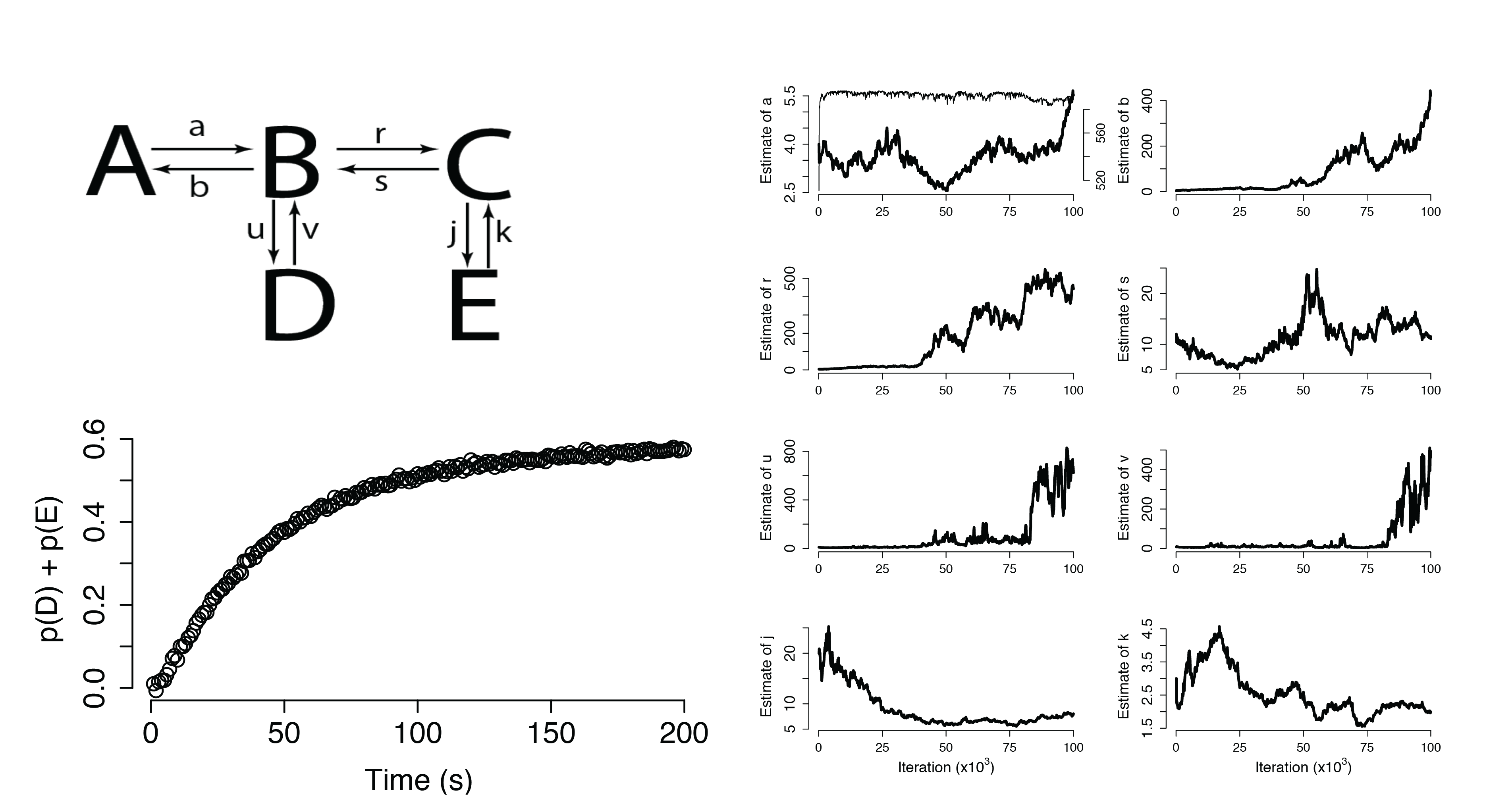
Additional Applications

Dynamical Systems (Non-Identifiable)

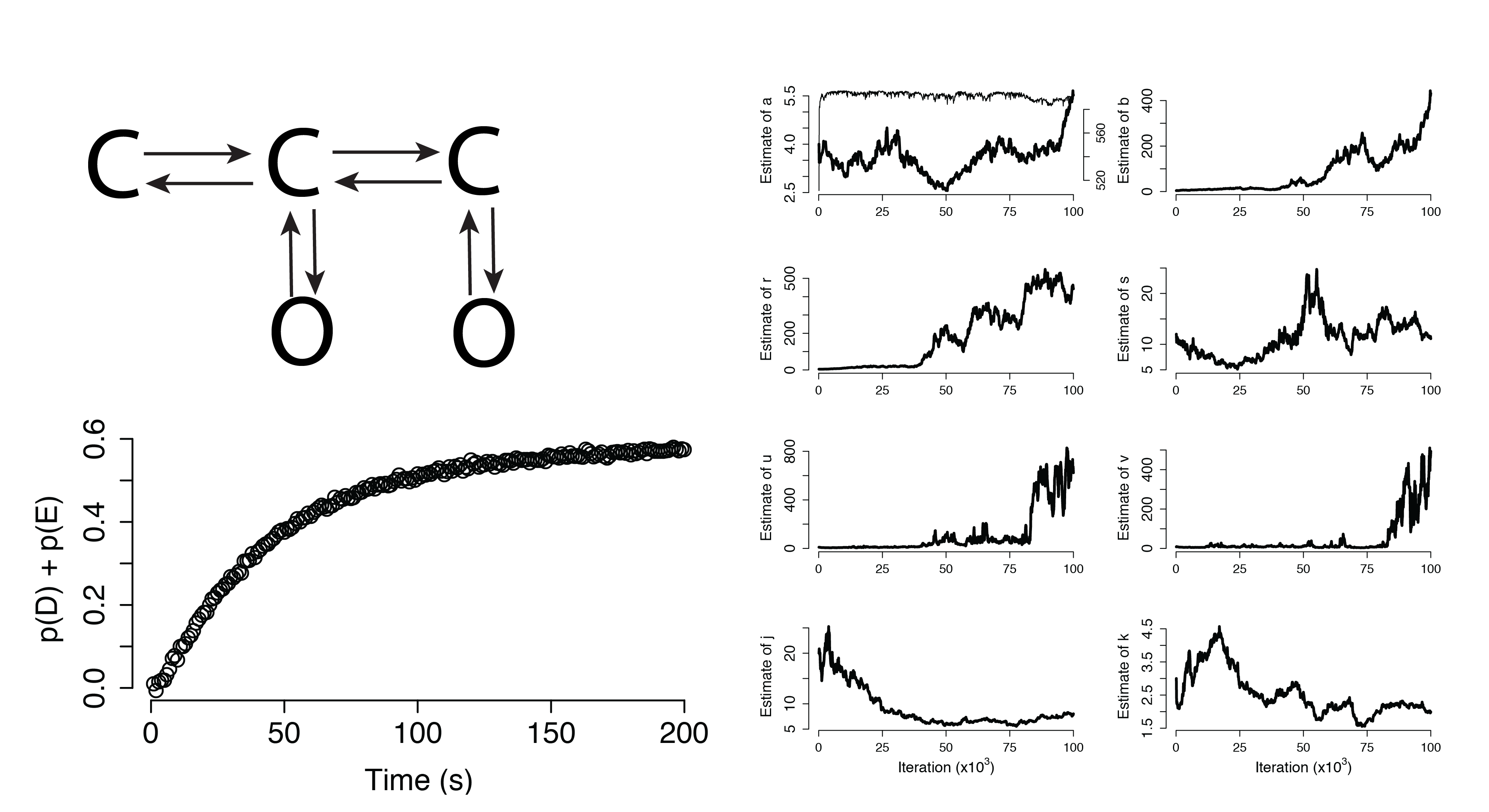
Model Selection and Experimental Design

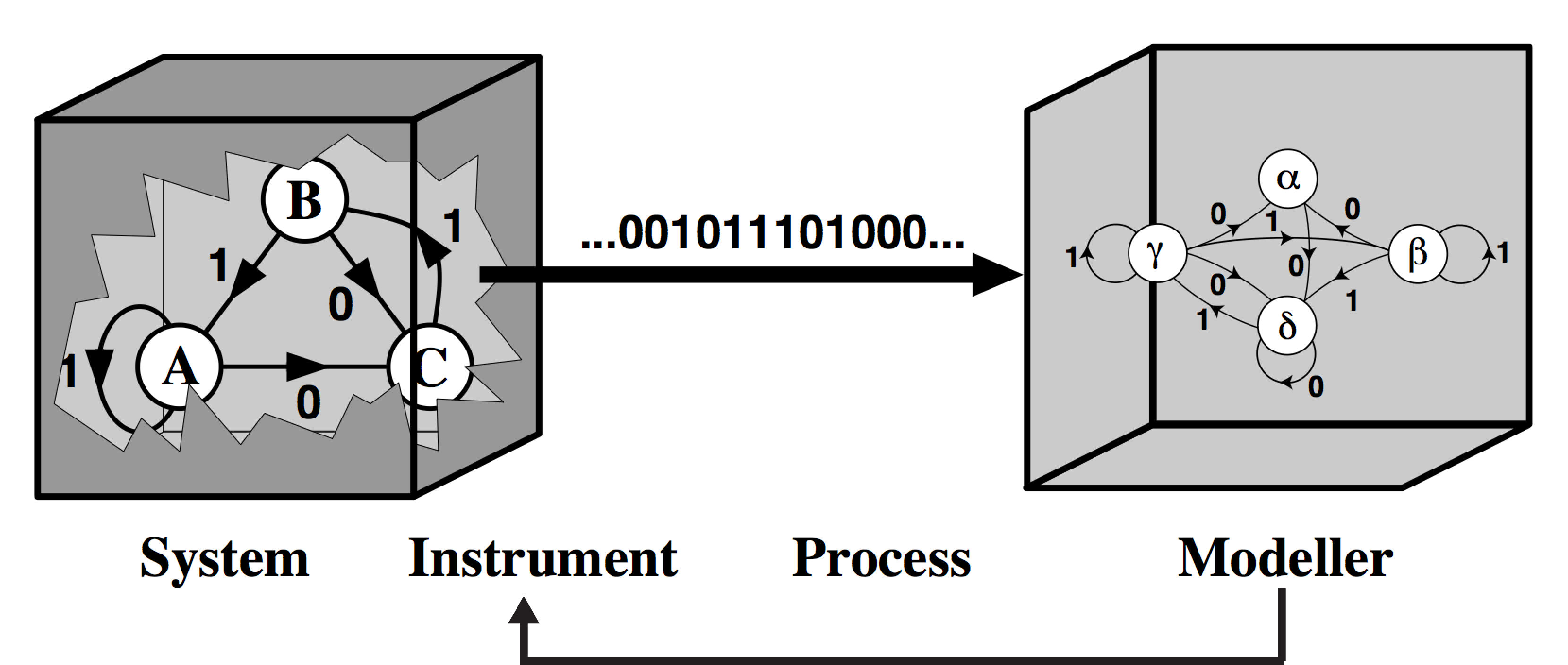
Modeling now becomes an iterative process, where non-identifiability forces innovative experimentation

Model Selection and Experimental Design



In the case of calcium binding to calmodulin, novel experiments have been developed to measure site specific binding curves (Jenni Greeson-Bernier).

Conclusions

  • Mechanistic models of proteins systems are important, though merely fitting data to models is insufficient: fits may not be unique
  • Non-identifiability is a concern not only for large and complex models, but also for extremely simple 2- and 3-parameter biophysical systems
  • New methods are required to determine the accuracy and identifiabilty of nonlinear models
  • Bayesian inference (& MCMC) is well suited to provide accurate parameter estimates and a direct assessment of identifiability
  • This approach will yield more accurate modeling and will force more innovative experimentation

Modeling Single Molecule Time Series Using Nonparametric Bayesian Inference

Single Molecule Measurements

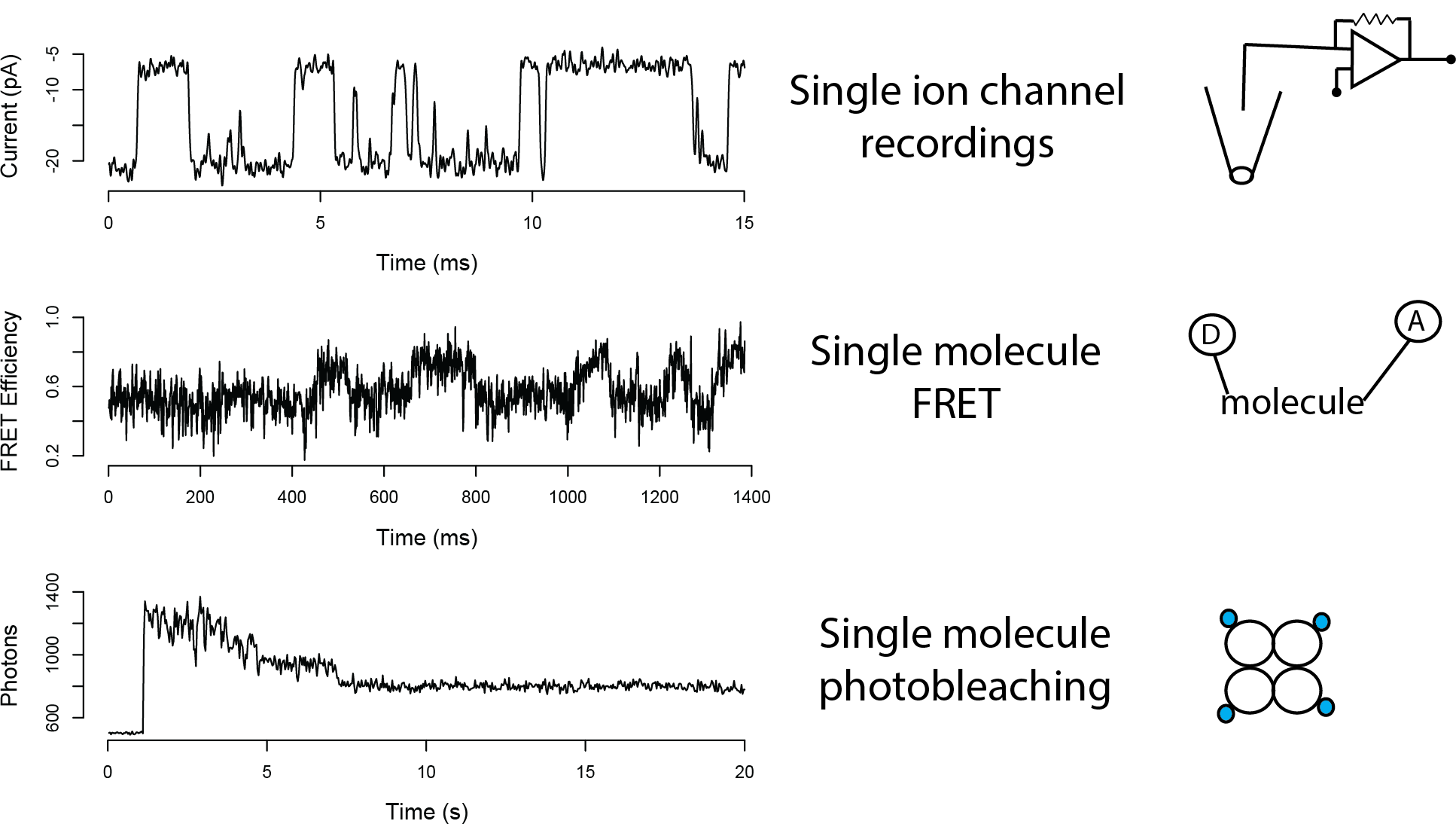
Modeling Single Molecule Time Series

Recall, we only need to account for some of the complexity available to the protein.


We imagine the protein accesses a relatively small number of biophysically distinct states.

Modeling Single Molecule Time Series

But how do we decide how many states and what model to use?

Nonparametric Bayes

Rely on a flexible class of infinite dimensional probability distributions - the Dirichlet process


We can extract structure from data, instead of assuming models beforehand


Structure might refer to hidden closed and open states in single channel recordings, or to conformational states in FRET traces, or to bleaching events in photobleaching traces

Dirichlet Process

Provides an infinite dimensional probability distribution


But has useful clustering properties when modeling finite data

Stick Breaking Process

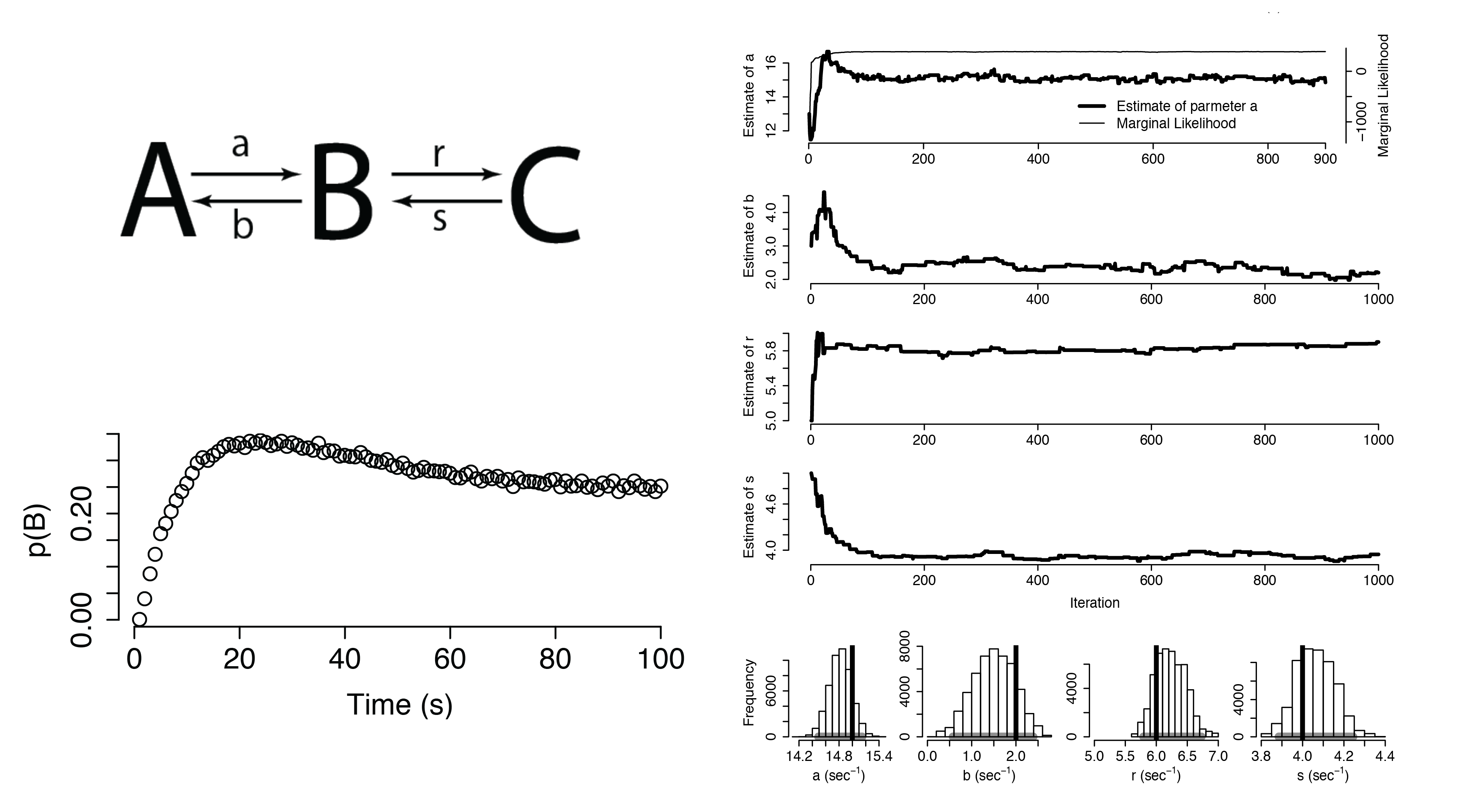
Hidden Markov Models

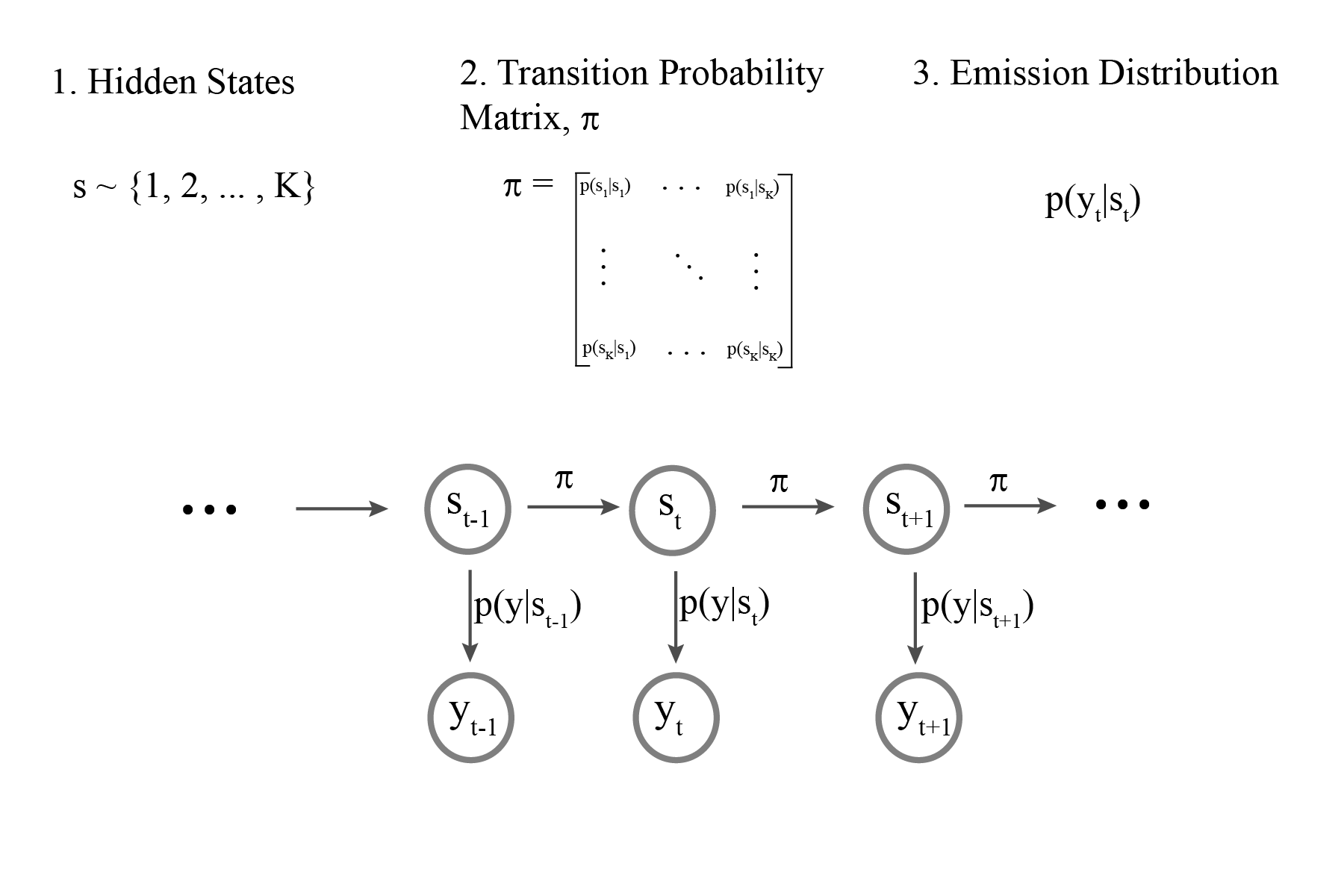
Hidden Markov Models

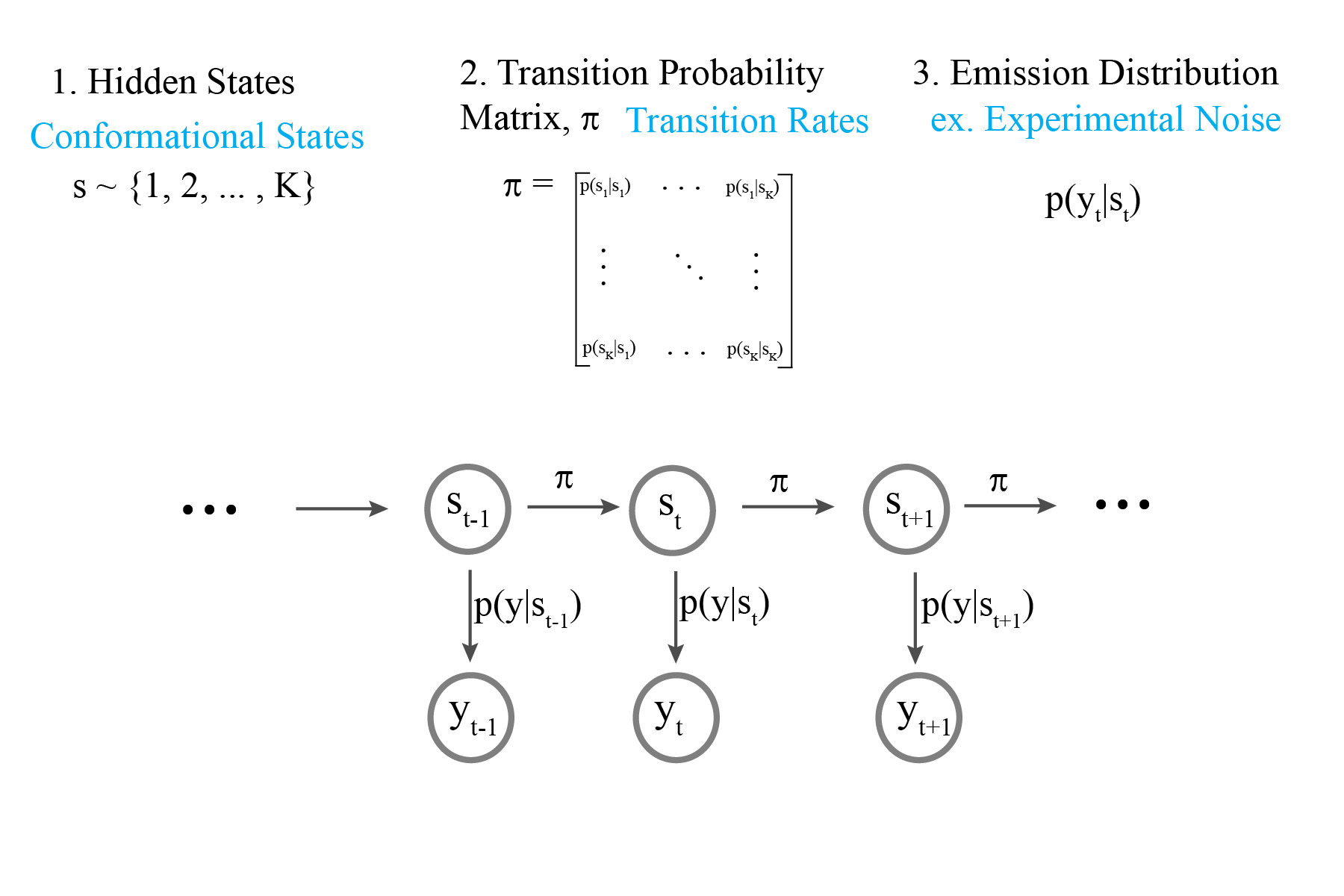
Infinite Hidden Markov Model

We now model the transition matrix as the bi-infinite Hierarchical Dirichlet Process


Our model now specifies transitions to and from an infinite number of hidden states


Using this infinite model allows us to discover the number of hidden states in a time series

Infinite Hidden Markov Model

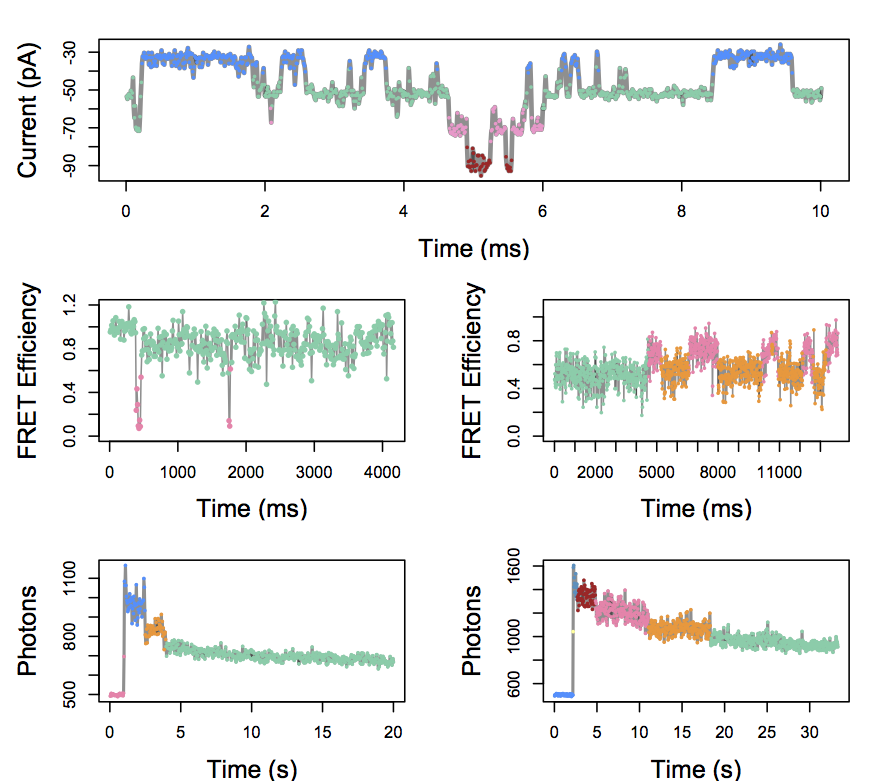
In each of these cases, we can detect the presence of distinct hidden states.

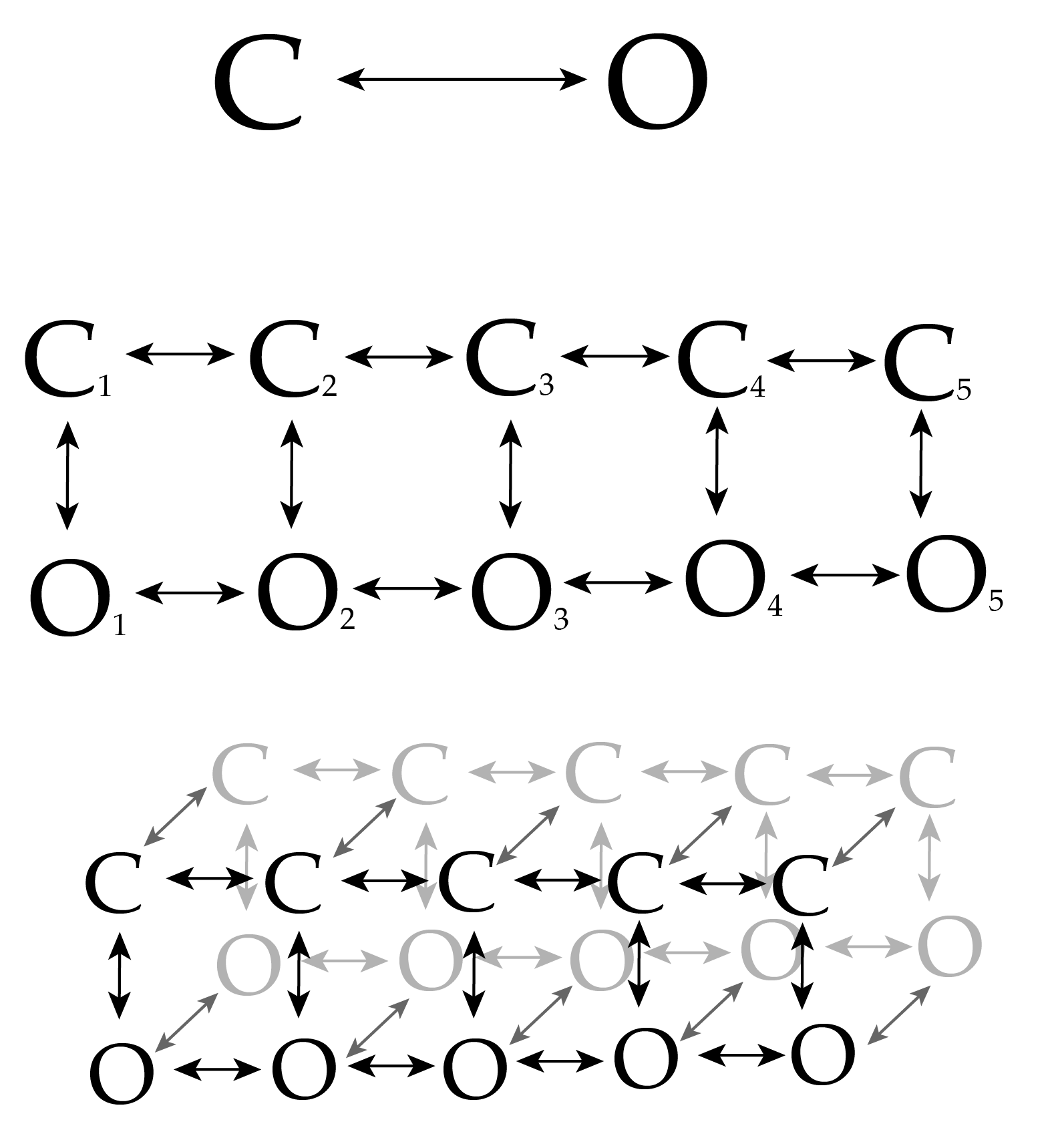
Aggregated Markov Model

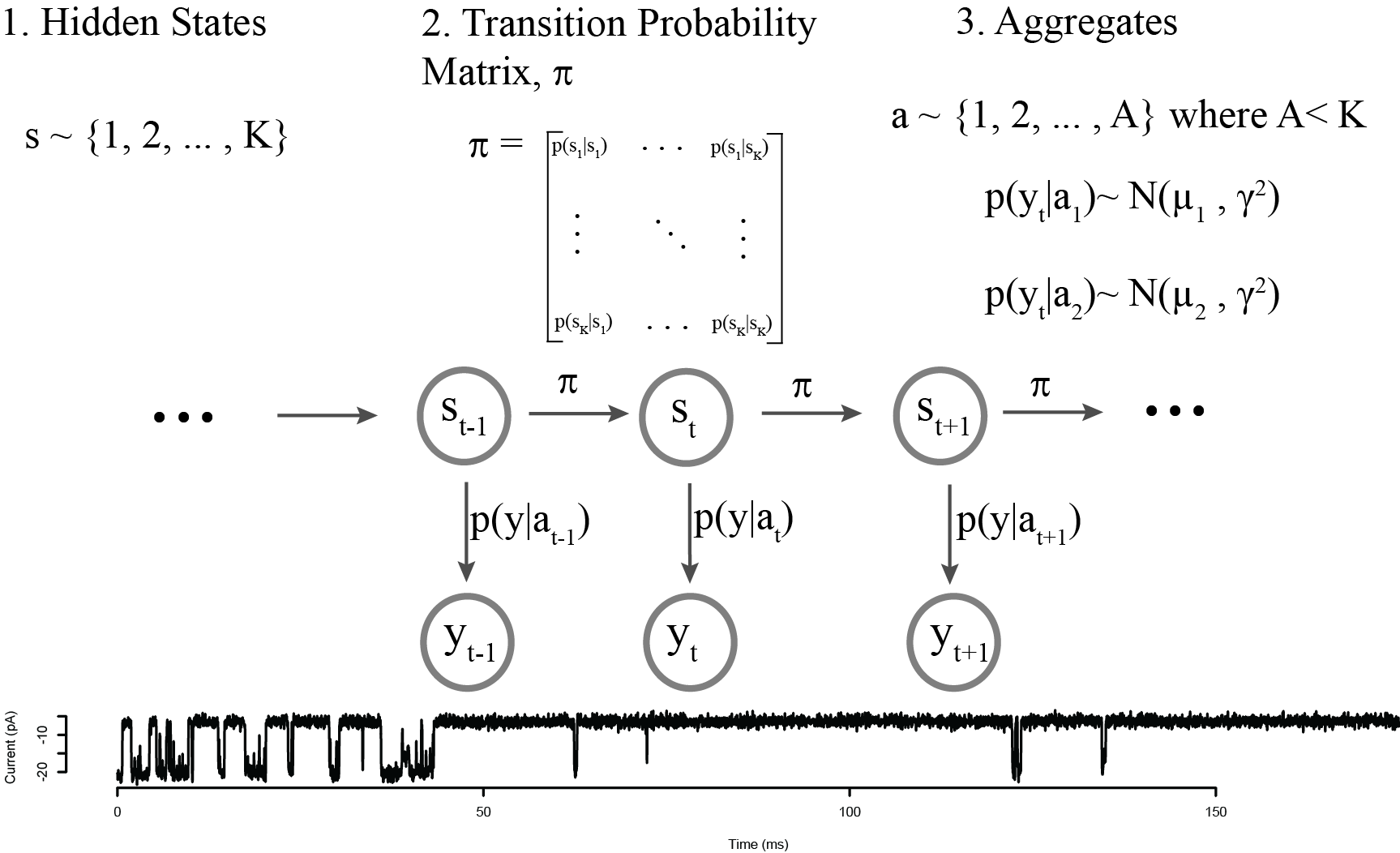
Infinite Aggregated Markov Model

We think there's only two conductance states (open and closed), but an unknown number of hidden states


Again, we now model the transition matrix as the bi-infinite Hierarchical Dirichlet Process


Our model now specifies transitions to and from an infinite number of hidden states, each of which appears as either open or closed


Using this infinite model allows us to discover the number of hidden states in single channel recording

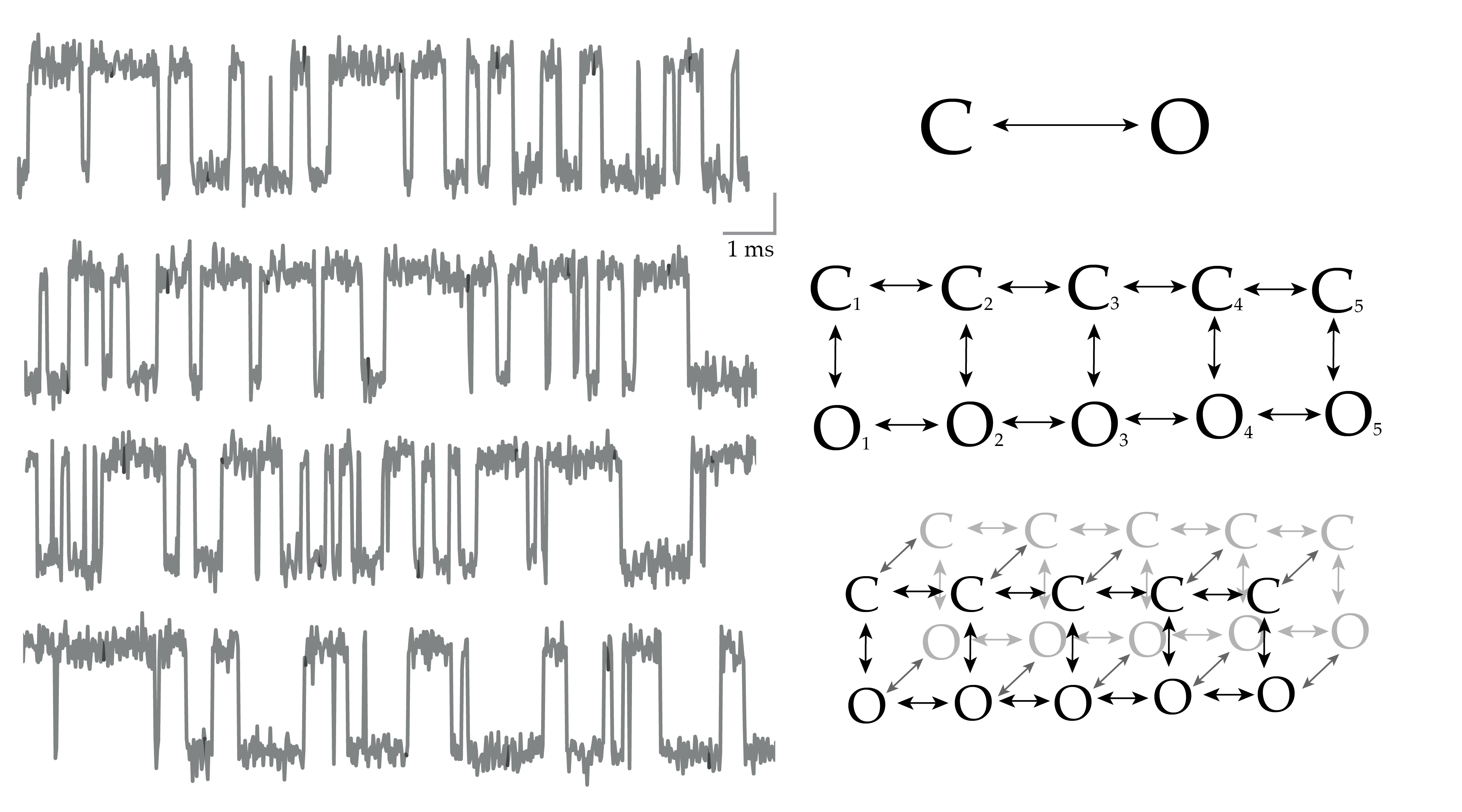
Infinite Aggregated Markov Model

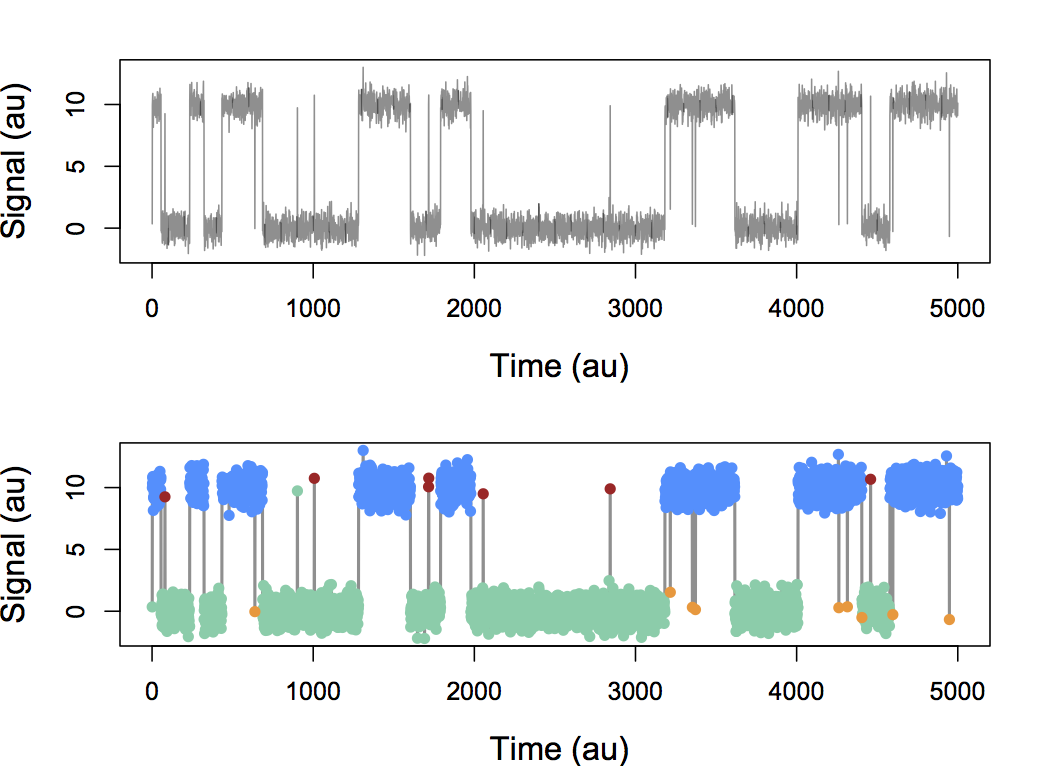
With simulated data, we can indeed discover hidden states based only on their different dynamics

Infinite Aggregated Markov Model

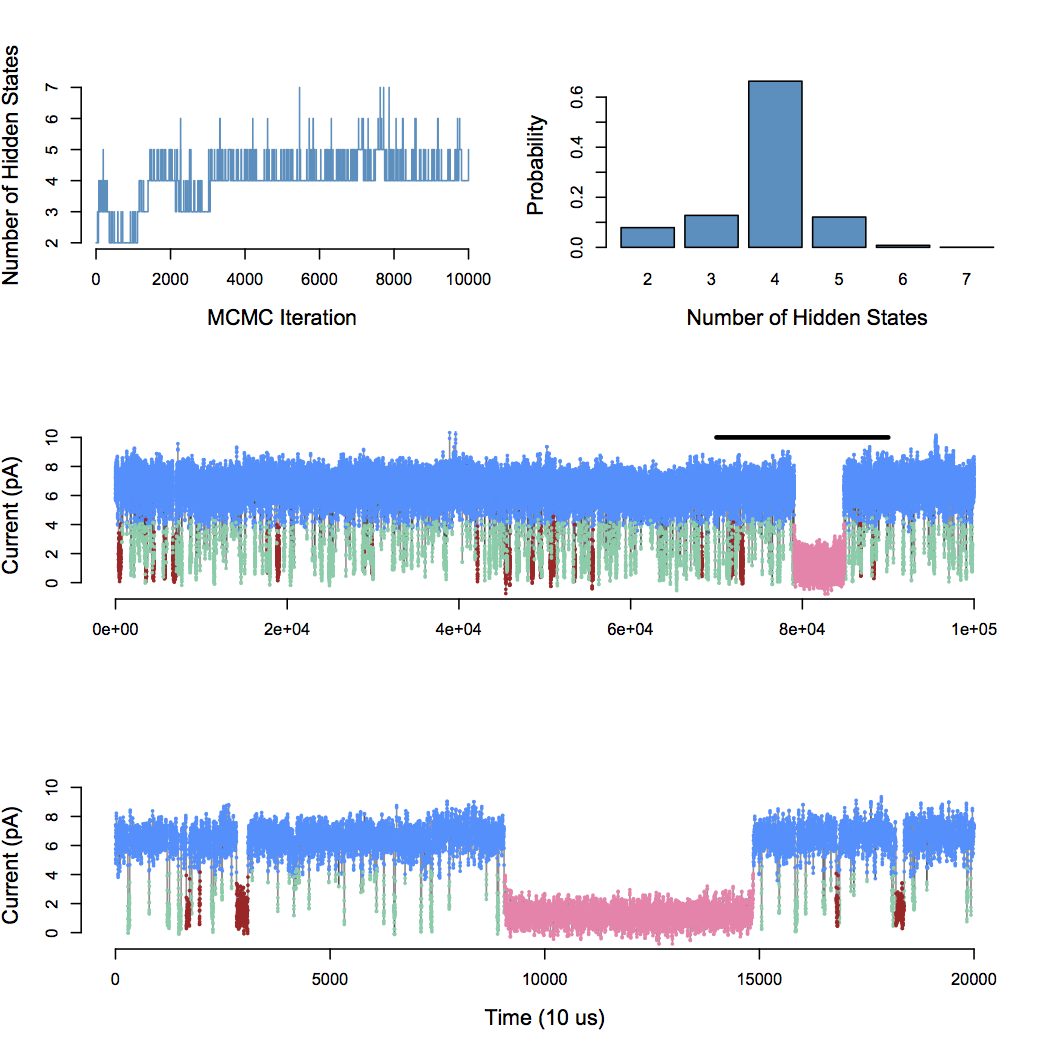
Application to BK channel data

Infinite Aggregated Markov Model

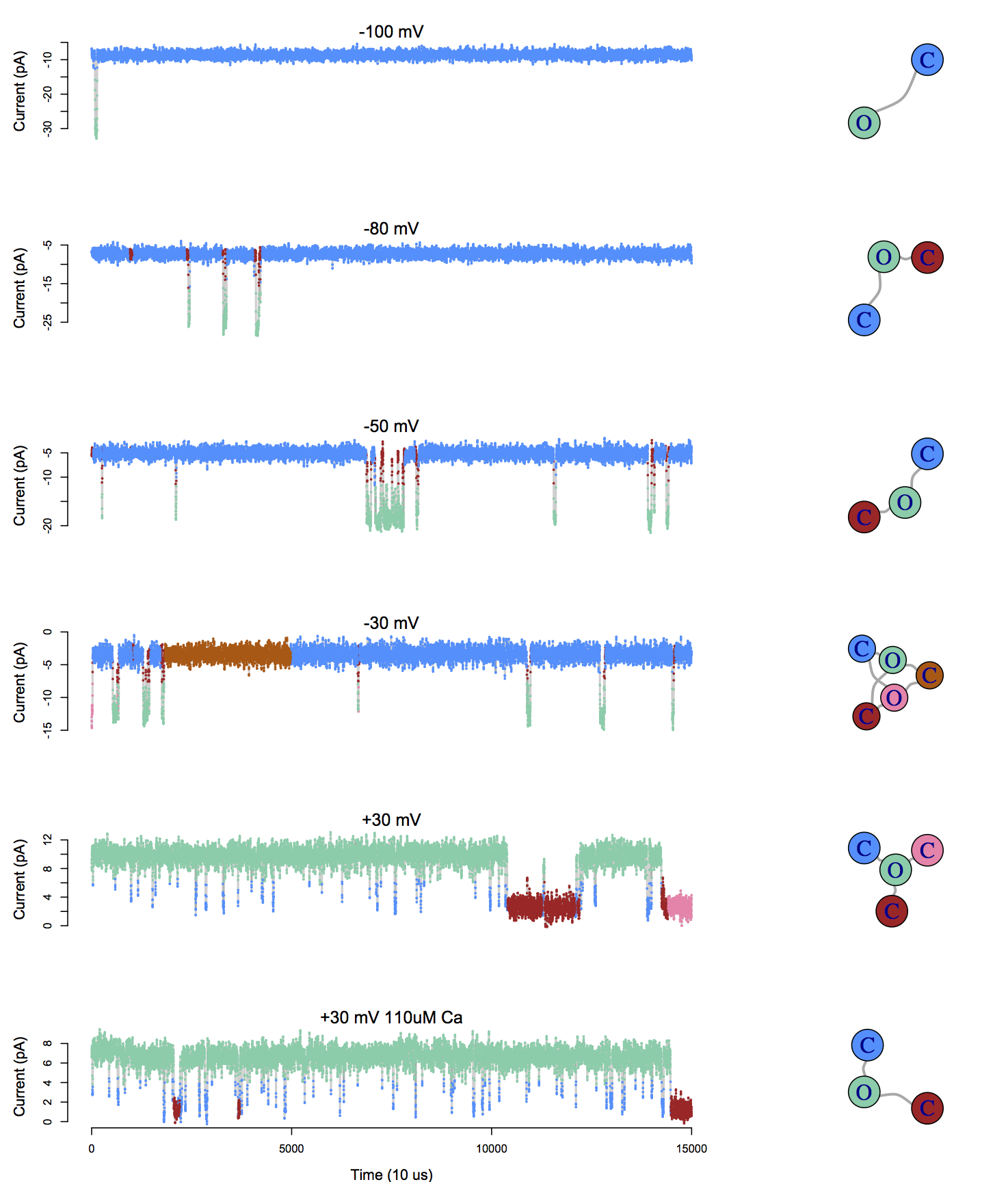
Nonparametric Bayes approach uncovers the complexity of channel gating

Conclusions

  • Powerful experimental methods allow us to measure the properties of proteins at the single molecule level
  • Developing rigorous and general tools for the analysis of such data remains an open challenge
  • Nonparametric Bayes methods can be used to discover structure in data instead of assuming models
  • These methods were demonstrated with diverse data sets including single channel recordings, single molecule FRET and single molecule photobleaching

Acknowledgements

Questions?